Như các bạn đã biết, BFS là thuật toán duyệt theo chiều rộng, thuật toán này có thể ra tìm đường đi ngắn nhất, trong mô hình đồ thị cơ bản chúng ta không chỉ dùng bfs trên các đỉnh thông thường, mà chúng ta còn có thể dùng BFS để giải quyết các bài toán trên ma trận, loang tìm kết quả từ 1 xâu,…
Trong bài viết này mình sẽ hướng dẫn các bạn cách giải quyết một bài toán trên ma trận có thể ứng dụng được bfs. Với những bạn vừa làm quen với đồ thị thì phải nắm được bài ví dụ minh họa dưới đây.
1. Yêu cầu kiến thức
Bài viết này yêu cầu bạn phải có kiến thức cơ bản về:
- BFS cơ bản
- Hiểu và biết cách sử dụng cấu trúc dữ liệu queue trong c++
- struct
2. Bài tập: Đếm bước đi của quân mã
Đề bài:
Trong cờ vua, một quân mã đứng tại một ô sẽ có 8 khả năng đi (các bạn xem hình minh họa)
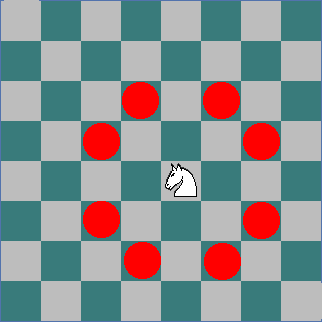
Yêu cầu: cho trước bạn một bàn cờ có kích thước m x n ô. Hãy đếm số bước đi ngắn nhất của một quân mã có tọa độ (x1,y1) di chuyển đến (x2,y2). Trong trường hợp không có cách nào để đến được (x2,y2) thì xuất ra giá trị -1.
Dữ liệu vào:
Dòng đầu gồm 2 số nguyên dương m, n (2 <= m, n <= 1000).
Dòng 2 gồm 2 số nguyên x1, y1 (1 <= x1 <= m, 1 <= y1 <= n).
Dòng 3 gồm 2 số nguyên x2, y2 (1 <= x2 <= m, 1 <= y2 <= n).
Dữ liệu ra: gồm một dòng duy nhất là kết quả bài toán.
3. Hướng dẫn giải bài
a. Lời giải chi tiết
Trong BFS duyệt đỉnh thông thường, mỗi đỉnh là 1 con số tuy nhiên trong bài toán này chúng ta phải coi mỗi ô trong ma trận chính là một đỉnh của đồ thị, còn các đỉnh kề của nó chính là 8 khả năng mà quân mã có thể đi được.
Như vậy để cho thuận tiện chúng ta tạo một kiểu dữ liệu struct data (hay record trong pascal) gồm các thông tin của một quân mã như sau:
- Quân mã đó đang ở tọa độ nào?
- Đã đi được bao nhiêu bước?
Đồng thời chúng ta tạo sẵn các hàm khởi tạo để thuận tiện hơn trong việc viết code (đối với c++)
struct data
{
int x, y, dem;
data()
{
dem=0;
}
data(int X, int Y, int Dem)
{
x=X; y=Y; dem=Dem;
}
};Tiếp theo, nếu trong bfs căn bản chúng ta có các nhãn để đánh dấu các đỉnh đã được duyệt (tránh tình trạng đi lại đỉnh đã duyệt) thì trong bài này chúng ta cũng có một mảng 2 chiều, để kiểm tra xem một ô trong bàn cờ, quân mã đã đi qua chưa?
Ở code bên dưới mình gọi a[i][j] là ô để xác định 1 quân cờ đã được duyệt qua chưa? Và tất nhiên ban đầu a[i][i]=0 với mọi i, j
Bắt đầu dùng BFS
– Mình thêm vào queue vị trí ban đầu của quân cờ, gồm các thông số tọa dộ x1, y1, và số bước đi ở thời điểm đó là 0. Và tiến hành đánh dấu ô (x1,y1) đã được đi qua : a[x1][y1]=1;
– Khi mà queue chưa rỗng, chúng ta lấy từ queue, data của quân cờ ra, và dễ dàng nhận thấy: từ 1 quân cờ được lấy ra sẽ có 8 khả năng đi.
- Lúc này các bạn cần xác định 8 khả năng đi được, như thế nào? dễ dàng nhận ra được, từ một quân cờ đang đứng tại tọa độ (u,v), 8 khả năng đi của nó là (u-2,v-1), (u-2, v+1), (u-1, v-2), (u-1,v+2),…v.v…
- sau khi các bạn nhận xét được các trường hợp như vậy, có thể xây dựng ngay 2 mảng chênh lệch dòng, và chênh lệch cột của các khả năng.
int cld[8]={-2,-2,-1,-1,1,1,2,2}; int clc[8]={-1,1,-2,2,-2,2,-1,1};- Như vậy chúng ta có thể lấy được đỉnh kề (tdx,tdy) của nó bằng cách dùng tdx = u + cld[i]; tdy = v+clc[i], với i là chỉ số của các trường hợp.
Từ bước trên chúng ta đã có thể lấy được các đỉnh kề (tdx, tdy) của đỉnh hiện đang xét. Như vậy chúng ta cũng thử lần lượt 8 khả năng đó, và tất nhiên từ 1 đỉnh được lấy ra từ queue có thể đi đến đỉnh kề của nó chỉ khi:
- đỉnh đó phải là đỉnh nằm trong bàn cờ, 1<=tdx && tdx <=m && 1<=tdy && tdy <=n
- đỉnh kề đó chưa được đi qua a[tdx][tdy]==0
Sau đó chúng ta đẩy vào queue một data mới với tọa độ (tdx,tdy) và số bước đi = số bước đi của đỉnh đi đến nó + 1 Và tiến hành kiểm tra (tdx,tdy) có phải là (x2,y2) không, nếu có thì chúng ta có thể kết thúc chương trình.
Sau khi queue rỗng mà vẫn không tìm được đường đi thì xuất -1.
b. Code tham khảo cho bài toán quân mã
#include <bits/stdc++.h>
using namespace std;
int a[2000][2000];
int m, n, tdx1 , tdy1 , tdx2 , tdy2;
int cld[8]={-2,-2,-1,-1,1,1,2,2};
int clc[8]={-1,1,-2,2,-2,2,-1,1};
struct data
{
int x, y, dem;
data()
{
dem=0;
}
data(int X, int Y, int Dem)
{
x=X; y=Y; dem=Dem;
}
};
int main()
{
queue <data> Q;
int m, n;
cin >> m >> n;
cin >> tdx1 >> tdy1;
cin >> tdx2 >> tdy2;
for (int i=1; i<=m; i++)
for (int j=1; j<=n; j++)
a[i][j]=0;
Q.push(data(tdx1,tdy1,0));
a[tdx1][tdy1]=1;
while (!Q.empty())
{
data tmp = Q.front();
Q.pop();
for (int k=0; k<8; k++)
{
int tdx = cld[k]+tmp.x;
int tdy = clc[k]+tmp.y;
if (1<=tdx && tdx <=m && 1<=tdy && tdy <=n && a[tdx][tdy]==0)
{
a[tdx][tdy]=1;
Q.push(data(tdx,tdy,tmp.dem+1));
if (tdx==tdx2 && tdy==tdy2)
{
cout << tmp.dem+1;
return 0;
}
}
}
}
cout << -1;
return 0;
}




