Trong lý thuyết đồ thị, việc tổ chức dữ liệu cho từng bài toán, thuật toán rất quan trọng, nó quyết định kích thước dữ liệu bài toán, thời gian thực tế của bài toán. Vì vậy trong bài viết này mình sẽ giới thiệu các bạn một số cách tổ chức dữ liệu trong đồ thị.
1. Tổng quan về ma trận kề trong lý thuyết đồ thị
Giả sử chúng ta có một đơn đồ thị vô hướng không trọng số, có n đỉnh. Chúng ta coi như các đỉnh được đánh số từ 1 đến n.
Tổ chức dữ liệu theo kiểu ma trận kề trong lý thuyết đồ thị bằng cách xây dựng ma trận vuông a[i,j] cấp n. Với:
- A[i][j] = 1 khi đồ thi của chúng ta có cạnh nối từ đỉnh i đến đỉnh j.
- A[i][j] = 0 khi đồ thị không có cạnh nối từ đỉnh i đến đỉnh j.
a. Đề bài ví dụ
Cho đồ thị đơn vô hướng, dữ liệu lấy từ input, dòng gồm 2 số n, m là số đỉnh và số cạnh của đồ thị, m dòng tiếp theo, mỗi dòng gồm 2 số u, v thể hiện cạnh nối giữa 2 đỉnh.
Ví dụ có n = 5 đỉnh, và có m = 4 cặp cạnh sau:
1 2
1 3
1 4
3 5
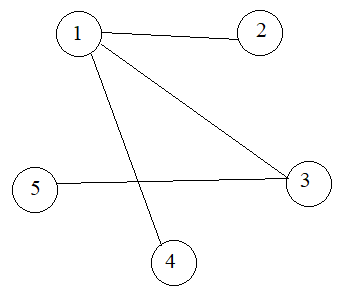
Vẽ đồ thị dựa trên mô tả đề bài
b. Dữ liệu ma trận kề được xây dựng
1 2 3 4 5 _________ 1|0 1 1 1 0 2|1 0 0 0 0 3|1 0 0 0 1 4|1 0 0 0 0 5|0 0 1 0 0
2. Nhập dữ liệu vào ma trận kề bằng c++
#define NMAX 100
int a[NMAX+1][NMAX+1];
int n, m, u, v;
cin >> n >> m;
for (int i=1; i<=n; i++)
for (int j=1; j<=n; j++)
a[u][v]=0; // Đầu tiên chúng ta coi đồ thị không có cạnh nào cả
for (int i=1; i<=m; i++)
{
cin >> u >> v;
a[u][v]=1;
a[v][u]=1;
}
Các bạn có thể tham khảo thêm về việc dùng ma trận kề trong BFS và DFS tại đây:
Thuật toán tìm kiếm theo chiều sâu DFS
Thuật toán tìm kiếm theo chiều rộng BFS
3. Ma trận kề có trọng số và có hướng
Bên trên chúng ta nói về đồ thị không trọng số, và vô hướng. Vậy nếu đồ thị có trọng số, hay có hướng thì sao?
- Nếu đồ thi có trọng số thì chúng ta thay a[u][v]=1 và a[v][u]=1 đó thành a[u][v]=a[v][u]=c (Với C chính là trọng số của cạnh đó). Điều này các bạn sẽ thấy rõ khi tiếp cận các thuật toán căn bản như Floyd, Dijkstra, Prim….
- Nếu đồ thì có hướng, và dữ liệu đề bài nói rõ cạnh đi từ u đến v thì bạn chỉ gán a[u][v]=1 và ko gán chiều ngược lại là được.
4. Ưu điểm và nhược điểm khi dùng ma trận kề trong lý thuyết đồ thị
Dễ dàng nhận thấy vì sử dụng mảng 2 chiều nên kích thước dữ liệu chúng ta tốn n^2 và độ phức tạp của dữ liệu này cũng là O(n^2).
Nhưng ma trận kề trong lý thuyết đồ thị cũng có ưu điểm là khi nhìn vào dữ liệu được tổ chức bằng ma trận kề, thì dễ dàng nhận biết được 2 đỉnh nào kề với nhau, chúng ta dễ cài đặt, và biết được bậc của từng đỉnh nếu đó là đồ thị đơn.




