Bài 3: Danh sách kề C++ Lý thuyết đồ thị

Để khắc phục yếu điểm của danh sách cạnh về việc tìm đỉnh kề, mà vẫn đảm bảo tổ chức dữ liệu tối ưu nhất phục vụ duyệt tìm trong đồ thị mà Danh sách kề được ra đời.

1. Ý tưởng danh sách kề

a. Ý tưởng

a.1 Tổ chức bằng mảng

Tổ chức dữ liệu kiểu danh sách kề là bạn sẽ lưu các đỉnh kề của một đỉnh vào các đoạn trong mảng để lưu trữ. Nếu có N đỉnh thì sẽ có N đoạn để lưu. Và chúng ta cần lưu lại chỉ số để quản lí phạm vi các đỉnh kề của đỉnh mà đoạn đó quản lí.

Các bạn xem hình ảnh bên dưới để hiểu rõ hơn ý tưởng này.

Gọi Head[i] là chỉ số kết thúc của đoạn quản lí đỉnh kề của i-1. Hay Head[i]+1 là chỉ số bắt đầu của đoạn quản lí đỉnh kề của i.

Như vậy, chỉ số của đoạn chứa các đỉnh kề của i là từ Head[i]+1 đến Head[i+1]

a.2 Tổ chức bằng danh sách liên kết

Việc tổ chức bằng danh sách liên kết, chúng ta sẽ có một mảng n ô, Mỗi ô chứa một pointer Node, pointer này gồm 2 thông tin là chỉ số đỉnh kề và pointer next tiếp theo. Tham khảo hình bên dưới (mục cài đặt bằng danh sách liên kết) để hiểu rõ hơn.

b. Ví dụ minh họa

Cho đồ thị đơn có hướng, có N đỉnh M canh. Dữ liệu các cạnh như sau:

1 2
1 3
2 4
2 3
2 5
3 5
3 6
4 5
5 6

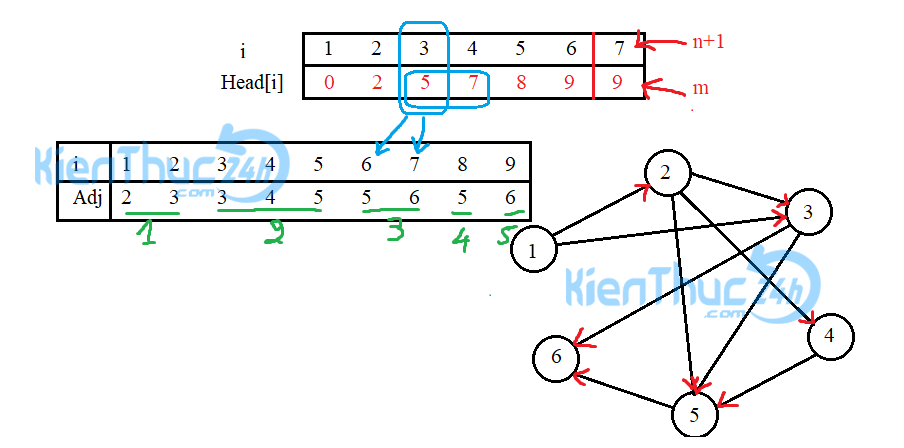
Ví dụ minh họa tổ chức danh sách kề bằng mảng một chiều

Trước tiên bạn chỉ cần hiểu các đỉnh kề của đỉnh u là Adj[v] với v=Head[u]+1……Head[u+1]

Như hình minh họa bên trên ở đỉnh số 3, mình có tô màu xanh ví dụ. Dựa vào việc xác định đỉnh kề bằng Head[] thì mình có được các đỉnh kề của 3 là Adj[ Head[3]+1 đến Head[3+1]]

Nếu viết bằng c++ thì mình lấy các đỉnh kề của đỉnh u bằng cách sau:

// Minh họa in các đỉnh kề của u
void indinhke(int u)
{
    for (int v=Head[u]+1; v<=Head[u+1]; v++)
        cout << Adj[v]<<endl;
}

c. Độ phức tạp

Độ phức tạp dữ liệu và thời gian là O(m) với m là số cạnh của đồ thị.

2. Cài đặt danh sách kề

a. Tổ chức bằng mảng bằng pascal / C++

Như những bài viết trước về tổ chức dữ liệu cho lý thuyết đồ thị, mình sẽ hướng dẫn các bạn đọc dữ liệu. Dòng đầu sẽ gồm 2 số N, và m.

Mô tả từng bước:

• Ban đầu Head[i]=0
• Đọc từng cạnh (u,v) và tăng Head[u]=Head[u]+1.
• Cộng dồn Head[i]=Head[i-1]+Head[i]. i=2->n+1;
• Lưu ý thêm Head[n+1] luôn m nếu đó là đồ thị có hướng.
• Duyệt qua các cạnh, Adj[Head[u]] = v; Head[u]=Head[u]-1;

Code tổ chức dữ liệu đồ thị bằng danh sách kề trong c++

#define NMAX 100
#define MMAX 1000

//Khai báo dữ liệu 
int x[MMAX], y[MMAX], Head[NMAX+2], Adj[MMAX+1];
int n, m, u, v;

// Đọc dữ liệu
cin >> n >> m;

// Gán Head[i]=0
for (int i=0; i<=n+1; i++)
    Head[i]=0;

for (int i=1; i<=m; i++)
{
    cin >> x[i] >> y[i];
    Head[x[i]]++;
}

for (int i=2; i<=n+1; i++)
    Head[i]=Head[i-1]+Head[i];

for (int i=1; i<=m; i++)
{ 
    Adj[Head[x[i]]]=y[i];
    Head[x[i]]--;
}

Code tổ chức dữ liệu đồ thị bằng danh sách kề trong Pascal

const nmax=100;
      mmax=1000;
type  data=longint;
// khai bao du lieu
var
    adj:array[0..mmax] of data;
    head,u,v:array[0..mmax+1] of data;

//doc du lieu
procedure docfile;
var     i,j:data;
begin
    read(n,m);
    fillchar(head,sizeof(head),0);
    for i:=1 to m do
        begin
            read(f,u[i],v[i]);
            inc(head[u[i]]); 
        end;
		
    for i:=2 to n+1 do
        head[i]:=head[i-1]+head[i];
		
    for i:=1 to m do
        begin
            adj[head[u[i]]]:=v[i]; 
            dec(head[u[i]]); 
        end; 
end;

Code bên trên là lưu trữ cạnh có hướng, nếu bạn muốn cạnh vô hướng bạn có thể xử lí thêm:

// Lúc nhập dữ liệu
Head[x[i]]++;
Head[y[i]]++;

Sau khi cộng dồn head, và tất nhiên MMAX phải tăng gấp đôi.

for (int i=1; i<=m; i++)
{ 
    Adj[Head[x[i]]]=y[i];
    Head[x[i]]--;
    
    Adj[Head[y[i]]]=x[i];
    Head[y[i]]--;
}

Nếu bạn muốn lưu thêm trọng số của cạnh, có thể tạo thêm một mảng có vai trò giống như adj, như lúc này chúng ta sẽ lưu trọng số của chúng.

b. Tổ chức danh sách liên kết

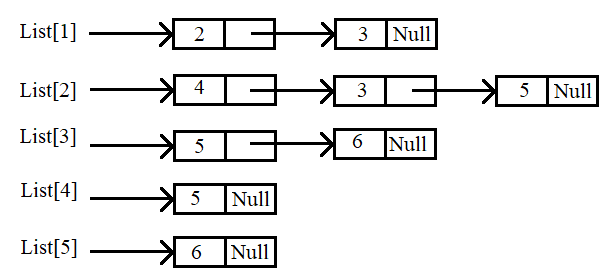
Tổ chức lưu trữ đồ thị bằng danh sách liên kết

struct Node
{
    int info;
    Node* pNext;
    Node()
    { 
        pNext=NULL; 
    }
}

Node* List[NMAX];
int u,v,m,n;

// Nhập số đỉnh và số cạnh
cin >> n >> m;
for (int i=1; i<=m; i++)
{
    cin >> u >> v;
    Node *p = new Node();
    p->info = v;

    if (List[u]==NULL)
        List[u] = p;
    else
    {
        p->pNext = List[u];
        List[u] = p;
    }
}

Duyệt đỉnh kề của u trong danh sách liên kết như thế nào ?

// Minh họa in các đỉnh kề của u
void indinhke(int u)
{
    Node *p = List[u];
    while (p!=NULL)
    {
        cout << p->info << endl;
        p=p->pNext;
    }
}

3. Ưu điểm và hạn chế của danh sách kề

– Ưu điểm của danh sách kề là chi phí duyệt và lưu trữ khá tối ưu. Đặc biệt là danh sách kề trong mảng.

– Cài đặt bài toán bằng danh sách kề tương đối dài hơn so với ma trận kề và danh sách cạnh.

– Đối với từng bài toán cụ thể, tùy vào dữ liệu bài toán cho, các bạn hãy lựa chọn cách tổ chức dữ liệu phù hợp nhất, không nhất thiết lúc nào cũng tổ chức danh sách kề.

4. Bài tập ứng dụng

Bài tập về danh sách kề nhìn chung các bạn có thể lấy các bài tập mình share ở bài về DFS, BFS về bản chất nó là như nhau.

Ngoài ra có thể tham khảo danh sách kề khi kết hợp với Prim heap: https://kienthuc24h.com/cay-khung-nho-nhat-qbmst-spoj-kruskal-prim-heap/