CRITICAL SPOJ- Thành phố trọng yếu

Đất nước Hạnh Phúc có N thành phố được nối với nhau bởi M đường nối hai chiều. Giữa hai thành phố bất kỳ chỉ có nhiều nhất một con đường.

Chính quyền nước này đưa ra một tiêu chí để đánh giá độ quan trọng của mỗi thành phố, theo đó độ quan trọng của một thành phố X được tính bằng số cặp thành phố A và B mà để di chuyển từ A đến B (và ngược lại) bắt buộc phải đi qua thành phố X.

Bạn hãy lập trình tính độ quan trọng trung bình của tất cả các thành phố.

Dữ liệu

Dòng đầu tiên chứa hai số nguyên N, M (1 <= N <= 20000, 0 <= M <= 200000).

M dòng tiếp theo mỗi dòng chứa 2 số nguyên u, v (1<=u,v <=N) mô tả một đường nối.

Kết quả

Gồm một số thực duy nhất là độ quan trọng trung bình của các thành phố, làm tròn đến 2 chữ số thập phân.

Ví dụ

Dữ liệu
5 5
1 2
2 3
3 4
4 5
5 3

Kết quả
1.40

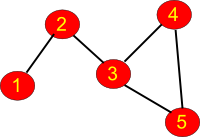
Giải thích: Độ quan trọng của các thành phố 1, 2, 3, 4, 5 lần lượt là 0, 3, 4, 0, 0. Độ quan trọng của thành phố 3 là 4 vì có 4 cặp thành phố mà khi di chuyển đến nhau cần đi qua thành phố 3: (1, 4), (1, 5), (2, 4), (2,5).

Thuật toán: sử dụng DFS+QHĐ trên topo

Nhận xét:tất cả những đỉnh không phải là đỉnh khớp đều có độ phức tạp bằng 0;

Trước tiên ta Dfs để tìm đỉnh khớp, thứ tự sắp xếp topo và các thành phần liên thông.

Gọi f[u] là số lượng con(cháu) của u trong cây gốc u,để làm được điều này t sẽ QHĐ ngược trên mảng sắp xếp topo;

Gọi g[u] là số lượng đỉnh không phải con(cháu) của u,lt[u] là thánh phần lien thông mà u nằm trong,sl[p] là số lượng đỉnh của thành phần liên thông p;

Với mỗi đỉnh khớp u và v1,v2,…vm là số lượng con của u,độ phức tạp của của u là

(tích của(f[vi]*(sl[lt[u]]-vi-1)))/2;

Mình nói hơi khó hiểu,có j thắc mắc các bạn để lại cmt và mình sẽ giải thíc cho nhé

//saker1417
#include <bits/stdc++.h>
#define maxn 30001
using namespace std;
vector < int > g[maxn];
int n,m,deg[maxn],cl[maxn],low[maxn],num[maxn],x[maxn],prev[maxn],f[maxn],sl[maxn],lt[maxn],slt=0;
int id=0,slx=0,khop[maxn];
void doc()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        int u,v;
        scanf("%d%d",&u,&v);
        deg[u]++;deg[v]++;
        g[u].push_back(v);
        g[v].push_back(u);
    }
}

void dfs(int u)
{
    sl[slt]++;lt[u]=slt;
    low[u]=num[u]=++id;
    x[++slx]=u;
    cl[u]=1;
    for(int i=0;i<deg[u];i++)
    {
        int v=g[u][i];
        if(prev[u]!=v)
        {
            if(cl[v]==0)
            {
                prev[v]=u;
                dfs(v);
                low[u]=min(low[u],low[v]);
            }else low[u]=min(low[u],num[v]);
        }
    }
}
void tinh()
{
    for(int i=1;i<=n;i++) if(cl[i]==0)slt++,dfs(i);
    for(int u=1;u<=n;u++)
    {
        int maxlow=-1,con=0;
        for(int i=0;i<deg[u];i++)
        {
            int v=g[u][i];
            if(prev[v]==u)
            {
                con++;
                maxlow=max(maxlow,low[v]);
            }
        }
        if(prev[u]==0) khop[u]=(con>1)?1:0;
        else if(maxlow>=num[u]) khop[u]=1;
    }
    for(int i=n;i>=1;i--)
    {
        int u=x[i];
        f[u]=1;
        for(int j=0;j<deg[u];j++)
        {
            int v=g[u][j];
            if(prev[v]==u) f[u]+=f[v];
        }
    }
    double kq=0;
    for(int u=1;u<=n;u++) if(khop[u]==1)
    {
        int dem=0;
        for(int i=0;i<deg[u];i++)
        {
            int v=g[u][i];
            if(prev[v]==u&&low[v]>=num[u]) kq+=(f[v])*(sl[lt[u]]-f[v]-1),dem+=f[v];
        }
        kq+=dem*(sl[lt[u]]-dem-1);
    }
    kq/=2;
    kq/=n;
    printf("%0.2lf",kq);
}

int main()
{
    ios::sync_with_stdio(false);
    doc();
    tinh();
}

😛